 |
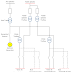
| Kısa Devre Akımlarının Hesabı -Jenerator, Trafo Besleme |
IEC 60909'a göre jeneratör ile beslenen trafodan oluşan basit tekhatta kısa devre akımlarının hesabına yönelik örnek yapılmıştır.
F1 barasında bir arıza tanımlansın.
DC bileşen F2:
F1 10 kV
Jeneratör reaktansı, IEC 60909'a göre subtransient reaktansa eşit alınabilir.
\[X_d^{''} = \frac{{x_d^{''}}}{{100\% }}.\frac{{{U_{rG}}^2}}{{{S_{rG}}}}\]
\[X_d^{''} = \frac{{0,16}}{{100\% }}.\frac{{{{10}^2}}}{{48}} = 0,3333\Omega\]
100 MVA'dan küçük çıkış gerilimi 1kV'tan büyük jeneratör için kurgusal bir direnç (RGf) hesaplanır. Bu değer jeneratör armature veya endüvi direncine eşit alınabilir.
\[{S_{rG}} < 100MVA\]
\[{U_{rG}} > 1kV\]
\[{R_{Gf}} = 0,07.X_d^{''}\]
\[{R_{Gf}} = 0,07.0,3333 = 0,02333\Omega\]
Bu değer jeneratör endüvi direncidir.
Jeneratör için düzeltme faktörü:
\[{K_G} = \frac{{{U_n}}}{{{U_{rG}}}}.\frac{{{c_{\max }}}}{{1 + x_d^{''}.\sqrt {1 - {{\cos }^2}{\varphi _{rG}}} }}\]
\[{K_G} = \frac{{10}}{{10}}.\frac{{1,1}}{{1 + 0,16.\sqrt {1 - 0,{9^2}} }} = 1,02828\]
\[{R_{Gf}} = {R_a}\]
\[\frac{{X_d^{''}}}{{{R_a}}} = \frac{{0,3333}}{{0,0233}} = 14,2587\]
Empedans kompleks sayılarla ifade edilebilir ve jenerator direnci ve reaktansından oluşur.
\[{\underline Z _G} = 0,0233 + j0,3333\Omega\]
Düzeltilmiş jeneratör empedansı için düzeltme faktörü ile çarpılır.
\[{\underline Z _{GK}} = 1,02828(0,0233 + jX0,3333)\Omega\]
F1 arızasına kadar arada başka bir şebeke bileşeni olmadığından jeneratör empedansı toplam empedansa eşittir.
\[{\underline Z _{GK}} = {\underline Z _{kF1}} = 0,023993 + j0,342762\Omega\]
Başlangıç simetrik kısa devre akımı 10 kV bara F1 için:
\[I_k^{''} = \frac{{c{U_n}}}{{\sqrt 3 {Z_k}}} = \frac{{c{U_n}}}{{\sqrt 3 \sqrt {{R_k}^2 + {X_k}^2} }}\]
\[I_{kF1}^{''} = \frac{{1,1.10}}{{\sqrt 3 .\sqrt {0,{{023993}^2} + 0,{{342762}^2}} }} = 18,4832kA\]
Akım karmaşık sayı ile de ifade edilebildiğinde açı değeri hesaplanabilir.
\[I_{kF1}^{''} = \frac{{1,1.10}}{{\sqrt 3 .(0,023993 + j0,342762)}} = \frac{{6,350853.(0,023993 - j0,342762)}}{{(0,{{023993}^2} + 0,{{342762}^2}})}\]
\[I_{kF1}^{''} = 53,79288.(0,023993 - j0,342762) = 1,290669 - j18,43813kA\]
\[\theta = \arctan \left( {\frac{{ - 18,43813}}{{1,290669}}} \right) = - 85,9958^\circ\]
Pik ya da darbe kısa devre akımının (ip) 10 kV F1 kısa devresi için bulunması
R/X değeri bulunur.
\[\kappa = 1,02 + 0,98{e^{ - 3R/X}}\]
\[{i_p} = \kappa \sqrt 2 {I_k}''\]
\[\frac{{{R_{kF1}}}}{{{X_{kF1}}}} = \frac{{0,023993}}{{0,342762}} = 0,07\]
Bu değer kurgusal direnç hesaplarken kullanılan sabittir.
\[\kappa = 1,02 + 0,98.{e^{ - 3.(0,07)}} = 1,8143\]
\[{i_p} = 1,8143.\sqrt 2 .18,483 = 47,426kA\]
Simetrik kesme akımının (Ib) 10 kV F1 arızası için bulunması
\[{I_b} = \mu .I_{k\max }^{''}\]
Zaman 0,1 saniye alınırsa \[\mu\]değeri formülü:
\[t = 0,10s\]
\[\mu = 0,62 + 0,72{e^{ - 0,32I_{kG}^{''}/{I_{rG}}}}\]
Jeneratör akımının hesabı:
\[{I_{rG}} = \frac{{{S_{rG}}}}{{\sqrt 3 .{U_{rG}}}}\]
\[{I_{rG}} = \frac{{48}}{{\sqrt 3 .10}} = 2,77128kA\]
Jeneratör kısa devre akımı, F1 hatasındaki kısa devre akımına eşittir.
\[I_{kF1}^{''} = I_{kG}^{''} = 18,483kA\]
Akımlar oranı katsayı hesabı için gereklidir.
\[\frac{{I_{kG}^{''}}}{{{I_{rG}}}} = \frac{{18,483}}{{2,7712}} = 6,6695\]
\[\mu = 0,62 + 0,72{e^{ - 0,32.6,6695}} = 0,70519\]
F1 noktasındaki simetrik kesme akımı:
\[{I_b}_{F1} = 0,70519.18,483 = 13,0343kA\]
Kararlı Hal Akımının(Ik) F1 arızası için bulunması
\[{I_{k\max }} = {\lambda _{\max }}.{I_{rG}}\]
Katsayı IEC 60909-1'de verilmektedir.
\[\lambda = \lambda \max = \frac{{{u_{f\max }}.\sqrt {1 + 2.{x_{dsat}}.\sin {\varphi _{rG}} + x_{dsat}^2} }}{{{x_{dsat}} - x_d^{''} + (1 + x_d^{''}.\sin {\varphi _{rG}}).{I_{rG}}/I_{kG}^{''}}}\]
Sinüs değeri güç faktörü 0.9 verildiğinden bulunabilir.
\[\sin {\varphi _{rG}} = 0,4358\]
\[\lambda \max = \frac{{1,3.\sqrt {1 + 2.1,5.0,4358 + 1,{5^2}} }}{{1,5 - 0,16 + (1 + 0,16.0,4358).2,7712/18,483}} = 1,8496\]
Kararlı hal akımı:
\[{I_{kF1}} = 1,8496.2,7712 = 5,1259kA\]
Kısa devre akımının DC bileşeninin F1 arızası için bulunması
Arıza noktasındaki R/X değeri, 50 Hz frekans, 0,1 sn zaman değeri ve başlangıç kısa devre akımı ile;
\[{i_{DC}} = \sqrt 2 .I_k^{''}.{e^{ - 2\pi .f.t.R/X}}\]
\[{i_{DC}} = \sqrt 2 .18,483.{e^{ - 2\pi .50.0,1.0,07}} = 2,898kA\]
Simetrik olmayan kısa devre akımı F1 hatası 10 kV bara
\[{I_{basyn}} = \sqrt {I_b^2 + i_{DC}^2}\]
\[{I_{basyn}} = \sqrt {13,{{0343}^2} + 2,{{898}^2}} = 13,352kA\]
F2 (0.38 kV)
Trafo empedansı 0,4 kV baz alınarak hesaplanır. Not: Bara gerilimi 0,38 kV
\[{Z_T} = \frac{{{u_{kr}}}}{{100\% }}.\frac{{{U_{rT}}^2}}{{{S_{rT}}}}\]
\[{Z_T} = \frac{{0,0715}}{{100\% }}.\frac{{0,{4^2}}}{5} = 0,002288\Omega\]
Trafo direnci
\[{R_T} = \frac{{{P_{krT}}}}{{\frac{{{S_{rT}}^2}}{{{U_{rT}}^2}}}}\]
\[{R_T} = \frac{{0,04175}}{{\frac{{{5^2}}}{{0,{4^2}}}}} = 0,0002672\Omega\]
Nisbi kısa devre gerilimini ya da kısa devre empedansının ( Z% ) nisbi omik bileşeni (%uRr) bulunabilir.
\[{u_{Rr}} = \frac{{{P_{krT}}}}{{{S_{rT}}}}.100\%\]
\[{u_{Rr}} = \frac{{0,04175}}{5} = 0,00835 = 0,835\%\]
Trafo reaktansı:
\[{X_T} = \sqrt {{Z_T}^2 - {R_T}^2}\]
\[{X_T} = \sqrt {0,{{002288}^2} - 0,{{0002672}^2}} = 0,002272344\Omega\]
Nispi reaktif bileşen Z% ( kısa devre empedansı bileşenidir)
\[{x_T} = \frac{{{X_T}}}{{\left( {\frac{{U_{rT}^2}}{{{S_{rT}}}}} \right)}}\]
\[{x_T} = \frac{{0,002272344}}{{\left( {\frac{{0,{4^2}}}{5}} \right)}} = 0,0710\]
Trafolar için düzeltme katsayısı empedans hesabında dikkate alınmalı.
\[{K_T} = 0,95.\frac{{{c_{\max }}}}{{1 + 0,6{x_T}}}\]
\[ c = 1,05\]
Alçak gerilim devrelerinde c değeri 1,05 alınır.
\[{K_T} = 0,95.\frac{{1,05}}{{1 + 0,6.0,0710}} = 0,9567\]
\[{\underline Z _{TK}} = {K_T}({R_T} + j{X_T})\]
\[{\underline Z _{TK}} = 0,9567(0,0002672 + j0,002272344)\]
\[{\underline Z _{TK}} = 0,000256 + j0,002174\Omega\]
F2 hata noktası için F1 arızası için kullanılan empedans 0,38 kV gerilim seviyesine dönüştürülür. Dönüştürme oranı 0,38 kV baranın bağlandığı trafo sarım sayısı oranının karesi ile yapılır. Yüksek gerilim tarafından alçak gerilim tarafına dönüştürme dönüştürme oranının karesinin tersi alınır.
\[{\textstyle{1 \over {t_r^2}}}\]
\[t_r^2 = \frac{{{{10}^2}}}{{0,{4^2}}} = {25^2}\]
\[{\underline Z _{kF1@0,38kV}} = \left( {0,023993 + j0,342762} \right).\frac{1}{{{{25}^2}}} = 3,{83.10^{ - 5}} + j0,00055\Omega\]
F2 hata noktasında toplam empedans:
\[{\underline Z _{kF2}} = {\underline Z _{TK}} + {\underline Z _{kF1@0,38kV}} = 0,0002940 + j0,00272\Omega\]
F2 noktası başlangıç kısa devre akımı 0,38 kV bara gerilimi kullanılarak bulunur.
\[I_k^{''} = \frac{{c{U_n}}}{{\sqrt 3 {Z_k}}}\]
\[I_{kF2}^{''} = \frac{{1,05.0,38}}{{\sqrt 3 .\sqrt {0,{{0002940}^2} + 0,{{00272}^2}} }} = 84,1266kA\]
Darbe kısa devre akımı F2:
\[\frac{{{R_{kF2}}}}{{{X_{kF2}}}} = \frac{{0,0002940}}{{0,00272\Omega }} = 0,1080\]
\[\kappa = 1,02 + 0,98{e^{ - 3.0,1080}} = 1,728\]
\[{i_p}_{F2} = 1,728.\sqrt 2 .84,1266 = 205,678kA\]
Kesme Akımı F2:
\[{I_b}_{F2} = I_{kF2}^{''} = 84,1266kA\]
Kararlı hal kısa devre akımı (Ik) F2:
\[{I_k}_{F2} = I_{kF2}^{''} = 84,1266kA\]
\[{i_{DC}} = \sqrt 2 .84,1266.{e^{ - 2\pi .50.0,1.0,1080}} = 3,998kA\]
Simetrik olmayan kesme akımı F2:
\[{I_{basyn}} = 84,2216kA\]
ETAP ile çözüm











0 Yorumlar