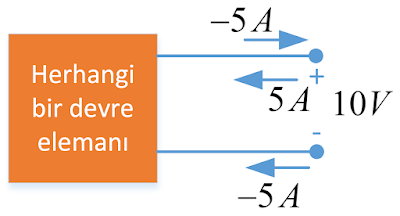
\[{i_R}(t) = - i(t)\]
Kirchhoff gerilim kanununda tekrar yazılırsa ( eksi işarete dikkat edilerek)
\[- ( - i(t))R + \frac{1}{C}\int\limits_{{t_0}}^t {i(t)dt} + {v_C}(0) = 0\]
Amaç DC besleme kesildiğinde kapasitör geriliminin fonksiyonunu elde etmek olduğundan türev alınıp gerilim ifadesi bulunmaya çalışılır.
\[+ \frac{{di(t)}}{{dt}}R + \frac{1}{C}i(t) = 0\]
Hala akım değerleri eşitlikte yer aldığından devre akım yönüne dikkate edilerek gerilimi elde etmek adına akım değerini direnç üzerinde bulmak daha kolay olduğundan;
\[- i(t) = \frac{{{v_C}(t)}}{R}\]
Türevde tekrar yazılırsa;
\[- \frac{{d{v_C}(t)}}{{dt}}.\frac{1}{R}.R - \frac{{{v_C}(t)}}{{RC}} = 0\]
\[\frac{{d{v_C}(t)}}{{dt}} = - \frac{{{v_C}(t)}}{{RC}}\]
İntegral almak için değişken düzenlenmesi yapılır. Zaman ve gerilim ifadeleri karşılıklı ifade edilir.
\[\frac{{d{v_C}(t)}}{{{v_C}(t)}} = - \frac{{dt}}{\begin{array}{l} RC\\ \end{array}}\]
\[{v_C}(0) = {V_0}\]
Kapasitör başlangıç gerilimi olsun.
\[{t_0} = 0\]
Zaman da sıfırdan başlasın.
İntegral alınırsa integral sınır değerleri değişkenlerin cinsinden olmalıdır. Burada gerilim ve zaman.
\[\int\limits_{Vo}^{{v_C}(t)} {\frac{{d{v_C}(t)}}{{{v_C}(t)}}} = \int\limits_0^t { - \frac{1}{{RC}}} dt\]
ln fonksiyonu integralden elde edilir
Hatırlatma :
\[ \int {\frac{1}{x}} dx = \ln x\]
\[ \int {dx} = x\]
----
\[\ln {v_C}(t)|_{{V_0}}^{{v_C}(t)} = - \frac{1}{{RC}}t|_0^t\]
\[{v_C}(t)\]
yazılırken bazı kaynaklarda
\[{v_C}'(t)\]
ya da
\[t'\]
yazılarak sınır değerle karışmaması istenmektedir. Değerler fonksiyonda yerine koyulan değerlerdir.
\[\ln (\frac{{{v_C}(t)}}{{{V_0}}}) = - \frac{1}{{RC}}t\]
ln 'den kurtulmak ve gerilim ifadesini tek başına elde etmek için e kullanılır.
\[{e^{\ln (\frac{{{v_C}(t)}}{{{V_0}}})}} = {e^{ - \frac{1}{{RC}}t}}\]
\[\frac{{{v_C}(t)}}{{{V_0}}} = {e^{ - \frac{1}{{RC}}t}}\]
\[{v_C}(t) = {V_0}{e^{ - \frac{1}{{RC}}t}}\]
Kapasitöre direnç bağlayıp şarj olduktan sonra DC'yi kesersek, direnç üzerinde ısı yayılarak kapasitör deşarj olur. Bu ifade deşarj ifadesidir ve kapasitör başlangıç gerilim değerine bağlıdır.
R değeri artılırsa
\[v(t) = i(t)R\]
göz önüne alındığında belli bir gerilimde akım düşer.
\[p(t) = i{(t)^2}R\]
olduğundan daha az güç ya da ısı yayılır.
\[t = RC\]
alınırsa gerilim belirli bir zamanda
\[v(t) = {V_0}\frac{1}{{{e^1}}} = \frac{{{V_0}}}{{0.3678}} = 2,718{V_0}\]
değerine düşer.
R ve/veya C arttığında örnek RC ifadesi 2 katı olsun, gerilim
\[{V_0}\frac{1}{{{e^{t/2t}}}} = \frac{{{V_0}}}{{{e^{0.5}}}} = \frac{{{V_0}}}{{0.6065}} = 1,648{V_0}\]
değerine daha fazla zaman geçtikten sonra düşer. Nedeni RC değeri zaman ekseninde de ileri yönlü ilerleme yaptırır. Başka ifade ile RC değeri bir zaman ifadesi olduğundan RC artarsa kapasitörde depolanan enerjiyi ısıya dönüştürmek için daha fazla zaman gerekir.
NOT:
R.C=ohm.farad
Ohm=volt/amper
farad=coulomb/volt
volt/amper x coulomb/volt=coulomb /amper
amper=coulomb/saniye
coulomb/coulomb/saniye=saniye
Referans: W.Hayt. J.E. Kemmerly, Engineering Circuit Analysis,
Çizim: Libre Office Draw
güç değerinin trafolarda sabit kalması gerekir. Trafo primer tarafı ile sekonder tarafı arasında güç eşittir ve trafolarda gerilim değişimi sağlanır. Bu nedenle akım ve gerilim sabit gücü sağlamak için birbiri ile ters orantılı değişir. Orta ve yüksek gerilim uygulamalarında sıklıkla karşımıza çıkar. 
