Aralarında iletim hattının indüktif reaktansı bulunan iki generatörlü, iki baralı bir sistem olsun.
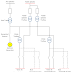
Şekilde bara gerilimleri kutupsal olarak, görünür güç ve generatörler arası akım karmaşık sayı olarak gösterilmektedir.
 |
| Şekil 1. Güç transferi eşdeğer sistem |
Besleme tarafındaki görünür güç
\[{{\tilde S}_1} = {P_1} + j{Q_1}\]
Alıcı taraftaki görünür güç
\[{{\tilde S}_2} = {P_2} + j{Q_2}\]
\[{{\tilde S}_2} = {P_2} + j{Q_2} = {{\tilde E}_2}{{\tilde I}^*}\]
\[\tilde I = \frac{{{{\tilde E}_1} - {{\tilde E}_2}}}{{jX}}\]
\[{P_2} + j{Q_2} = {{\tilde E}_2}{\left[ {\frac{{{{\tilde E}_1} - {{\tilde E}_2}}}{{jX}}} \right]^*}\]
\[{{\tilde E}_2} = {E_2}\cos 0 + j{E_2}\sin 0\]
sin0=0, cos0=1 değerini alır.
\[{{\tilde E}_1} = {E_1}\cos \delta + j{E_1}\sin \delta\]
\[{P_2} + j{Q_2} = {E_2}{\left[ {\frac{{{E_1}\cos \delta + j{E_1}\sin \delta - {E_2}}}{{jX}}} \right]^*}\]
Formülde karmaşık sayının eşleniği alınacağından
\[- jX\]
ile çarpım uygulanarak önce karmaşık sayı daha düzgün hale getirilir.
\[= {E_2}{\left[ {\frac{{{E_1}\cos \delta ( - jX) + j{E_1}\sin \delta ( - jX) - {E_2}( - jX)}}{{jX( - jX)}}} \right]^*}\]
\[= {E_2}{\left[ {\frac{{ - jX{E_1}\cos \delta }}{{{X^2}}} + \frac{{{E_1}X\sin \delta }}{{{X^2}}} + \frac{{j{E_2}X}}{{{X^2}}}} \right]^*}\]
\[= {E_2}{\left[ {\frac{{{E_1}\sin \delta - j\left( {{E_1}\cos \delta - {E_2}} \right)}}{X}} \right]^*}\]
eşlenik ile aradaki eksi işareti artı ile değiştirilir.
\[= {E_2}\left[ {\frac{{{E_1}\sin \delta + j\left( {{E_1}\cos \delta - {E_2}} \right)}}{X}} \right]\]
\[{P_2} + j{Q_2} = \frac{{{E_2}{E_1}\sin \delta + j\left( {{E_2}{E_1}\cos \delta - {E_2}^2} \right)}}{X}\]
\[{P_2} + j{Q_2} = \frac{{{E_1}{E_2}\sin \delta }}{X} + \frac{{j\left( {{E_1}{E_2}\cos \delta - {E_2}^2} \right)}}{X}\]
\[{P_2} = \frac{{{E_1}{E_2}\sin \delta }}{X}\]
\[{Q_2} = \frac{{{E_1}{E_2}\cos \delta - {E_2}^2}}{X}\]
Yukarıdaki denklemlere göre 1 nolu generatörden 2 nolu generatöre iletim hattı üzerinden güç transferi durumunda ikinci generatördeki aktif ve reaktif güçlerin bulunması ile ikinci generatöre aktarılan reaktif güç, birinci ve ikinci generatörün gerilimine, yük açısına ve iletim hattının reaktansına bağlıdır.
1 nolu generatördeki aktif ve reaktif güçler de aynı formülle bulunabilir.
\[{{\tilde S}_1} = {P_1} + j{Q_1} = {{\tilde E}_1}\tilde I*\]
\[{{\tilde S}_1} = {{\tilde E}_1}{\left[ {\frac{{{{\tilde E}_1} - {{\tilde E}_2}}}{{jX}}} \right]^*}\]
\[{{\tilde S}_1} = ({E_1}\cos \delta + j{E_1}\sin \delta ){\left[ {\frac{{{E_1}\cos \delta + j{E_1}\sin \delta - {E_2}\cos 0 - j{E_2}\sin 0}}{{jX}}} \right]^*}\]
\[{{\tilde S}_1} = ({E_1}\cos \delta + j{E_1}\sin \delta ){\left[ {\frac{{ - jX{E_1}\cos \delta - {j^2}X{E_1}\sin \delta + jX{E_2}}}{{ - {j^2}{X^2}}}} \right]^*}\]
\[{{\tilde S}_1} = ({E_1}\cos \delta + j{E_1}\sin \delta ){\left[ {\frac{{ - j{E_1}\cos \delta + {E_1}\sin \delta + j{E_2}}}{X}} \right]^*}\]
\[{{\tilde S}_1} = ({E_1}\cos \delta + j{E_1}\sin \delta ){\left[ {\frac{{{E_1}\sin \delta - j({E_1}\cos \delta - {E_2})}}{X}} \right]^*}\]
\[{{\tilde S}_1} = ({E_1}\cos \delta + j{E_1}\sin \delta )\left[ {\frac{{{E_1}\sin \delta + j({E_1}\cos \delta - {E_2})}}{X}} \right]\]
\[+ \left[ {\frac{{j{E_1}^2{{\sin }^2}\delta + {j^2}{E_1}^2\sin \delta \cos \delta - {j^2}{E_1}{E_2}\sin \delta }}{X}} \right]\]
\[{{\tilde S}_1} = \left[ {\frac{{{E_1}^2\cos \delta \sin \delta - {E_1}^2\sin \delta \cos \delta + j{E_1}^2{{\cos }^2}\delta + j{E_1}^2{{\sin }^2}\delta }}{X}} \right]\]
\[+ \left[ {\frac{{{E_1}{E_2}\sin \delta - j{E_1}{E_2}\cos \delta }}{X}} \right]\]
\[{\cos ^2}\delta + {\sin ^2}\delta = 1\]
\[j{E_1}^2{\cos ^2}\delta + j{E_1}^2{\sin ^2}\delta = j{E_1}^2\]
\[{{\tilde S}_1} = {P_1} + j{Q_1} = \frac{{{E_1}{E_2}\sin \delta + j({E_1}^2 - {E_1}{E_2}\cos \delta )}}{X}\]
\[{P_1} = \frac{{{E_1}{E_2}\sin \delta }}{X}\]
\[{Q_1} = \frac{{{E_1}^2 - {E_1}{E_2}\cos \delta }}{X}\]
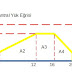
Reaktif güç transferinde gerilime göre değişim
 |
| Şekil 2. Güç akışı fazör diyagramları |








0 Yorumlar