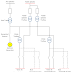
The equations and phasor diagram of T method of medium length transmission lines will be obtained. For this purpose the figure shows the one phase of three phase lines.
T Method Equations
The circuit can be separated in three parts based on inputs and outputs to obtain equations for T method.
Basic equation in matrice will be obtained by A, B, C, D parameters.
\[\left( \begin{array}{l}Vs\\{I_S}\end{array} \right) = \left( {\begin{array}{*{20}{c}}A&B\\C&D\end{array}} \right).\left( \begin{array}{l}{V_R}\\{I_R}\end{array} \right)\]
In section 1 output of the circuit will be V1 and Is1 when inputs are Vs and Is. However, consider all the electrical parameters in complex form a + jb, which means there will be a phase angle and magnitude of the currents and voltages.
\[\begin{array}{l} - {V_S} + {I_{S1}}\frac{Z}{2} + {V_1} = 0\\{V_S} = {V_1} + \frac{Z}{2}{I_{S1}}\\{I_S} = 0.{V_1} + {I_{S1}}\\\left( \begin{array}{l}{V_S}\\{I_S}\end{array} \right) = \left( {\begin{array}{*{20}{c}}1&{\frac{Z}{2}}\\0&1\end{array}} \right)\left( \begin{array}{l}{V_1}\\{I_{S1}}\end{array} \right)\end{array}\]
In section 2, if we use the inputs as V1 and Is1 which previously are the outputs of section 1, then the outputs will be V2 and Is2. As it is seen V2=V0 but no need to use for the matrice. V0 will be used for phasor diagram later.
\[\begin{array}{l}{V_1} = {V_2} + 0.{I_{S2}}\\{I_{S1}} = {I_Y} + {I_{S2}}\\{I_{S1}} = Y.{V_2} + {I_{S2}}\\\left( \begin{array}{l}{V_1}\\{I_{S1}}\end{array} \right) = \left( {\begin{array}{*{20}{c}}1&0\\Y&1\end{array}} \right)\left( \begin{array}{l}{V_2}\\{I_{S2}}\end{array} \right)\end{array}\]
Remember the basic formula.
\[\begin{array}{l}V = IZ\\I = V/Z\\Y = 1/Z\\I = VY\end{array}\]
In section 3, V2 and Is2 , the outputs of section 2, will be the inputs and finally IR and VR will be the outputs in similar way.
\[\begin{array}{l}{V_2} = {V_R} + \frac{Z}{2}{I_R}\\{I_{S2}} = 0.{V_R} + {I_R}\\\left( \begin{array}{l}{V_2}\\{I_{S2}}\end{array} \right) = \left( {\begin{array}{*{20}{c}}1&{\frac{Z}{2}}\\0&1\end{array}} \right)\left( \begin{array}{l}{V_R}\\{I_R}\end{array} \right)\end{array}\]
Consider all matrices again, and replace the values into previous ones.
\[\left( \begin{array}{l}{V_1}\\{I_{S1}}\end{array} \right) = \left( {\begin{array}{*{20}{c}}1&0\\Y&1\end{array}} \right)\left( {\begin{array}{*{20}{c}}1&{\frac{Z}{2}}\\0&1\end{array}} \right)\left( \begin{array}{l}{V_R}\\{I_R}\end{array} \right)\]
\[\left( \begin{array}{l}{V_S}\\{I_S}\end{array} \right) = \left( {\begin{array}{*{20}{c}}1&{\frac{Z}{2}}\\0&1\end{array}} \right)\left( {\begin{array}{*{20}{c}}1&0\\Y&1\end{array}} \right)\left( {\begin{array}{*{20}{c}}1&{\frac{Z}{2}}\\0&1\end{array}} \right)\left( \begin{array}{l}{V_R}\\{I_R}\end{array} \right)\]
\[\left( \begin{array}{l}{V_S}\\{I_S}\end{array} \right) = \left( {\begin{array}{*{20}{c}}{1 + \frac{{ZY}}{2}}&{0 + \frac{Z}{2}}\\{0 + Y}&{0 + 1}\end{array}} \right)\left( {\begin{array}{*{20}{c}}1&{\frac{Z}{2}}\\0&1\end{array}} \right)\left( \begin{array}{l}{V_R}\\{I_R}\end{array} \right)\]
\[\left( \begin{array}{l}{V_S}\\{I_S}\end{array} \right) = \left( {\begin{array}{*{20}{c}}{1 + \frac{{ZY}}{2}}&{\left( {1 + \frac{{ZY}}{2}} \right).\frac{Z}{2} + \frac{Z}{2}}\\Y&{1 + \frac{{ZY}}{2}}\end{array}} \right)\left( \begin{array}{l}{V_R}\\{I_R}\end{array} \right)\]
\[\begin{array}{l}\left( {1 + \frac{{ZY}}{2}} \right).\frac{Z}{2} + \frac{Z}{2} = \frac{Z}{2}\left( {1 + \frac{{ZY}}{2} + 1} \right)\\ = Z\left( {1 + \frac{{ZY}}{4}} \right)\end{array}\]
T method equation :
\[\left( \begin{array}{l}{V_S}\\{I_S}\end{array} \right) = \left( {\begin{array}{*{20}{c}}{1 + \frac{{ZY}}{2}}&{Z\left( {1 + \frac{{ZY}}{4}} \right)}\\Y&{1 + \frac{{ZY}}{2}}\end{array}} \right)\left( \begin{array}{l}{V_R}\\{I_R}\end{array} \right)\]
Phasor Diagram of T Method
Equations to obtain phasors. Impedance will be in complex form with angle and magnitude as well.
\[\left| {\frac{Z}{2}} \right|\angle \theta \]
\[\left| {{I_R}} \right|\angle - {\phi _R}\]
Inductive current lags reference voltage by negative sign angle. VR receiving voltage is the reference voltage for phasor diagram.
Based on right side of the circuit, voltage drop can be calculated by V0.
\[\overline {{V_0}} = \overline {{V_R}} + \overline {\Delta {V_2}} = \left| {{V_0}} \right|\angle {\delta _0}\]
Sending current with receiving current can be written in complex form. Notice that admitance with V0 which means the angle of the current flowing through admitance IY angle is 90 degree.
\[\begin{array}{l}\overline {{I_S}} = \overline {{I_Y}} + \overline {{I_R}} = \overline Y .\overline {{V_0}} + \overline {{I_R}} \\\overline {{I_S}} = \left| Y \right|\angle 90^\circ .\left| {{V_0}} \right|\angle {\delta _0} + \left| {{I_R}} \right|\angle - {\phi _R}\\\overline {{I_S}} = \left| {Y{V_0}} \right|\angle \left( {90^\circ + {\delta _0}} \right) + \left| {{I_R}} \right|\angle - {\phi _R}\end{array}\]
Voltage drop in left side of the circuit:
\[\overline {\Delta {V_1}} = \overline {{I_S}} \frac{{\overline Z }}{2} = \left| {{I_S}} \right|\angle - {\phi _S}\left| {\frac{Z}{2}} \right|\angle \theta = \left| {{I_S}\frac{Z}{2}} \right|\angle \theta - {\phi _S}\]
Sending voltage with left side voltage drop and V0 . Consider VS angle with respect to VR receiving voltage which is reference voltage for phasor diagram.
\[{\overline V _S} = \overline {{V_0}} + \overline {\Delta {V_1}} = \left| {{V_S}} \right|\angle {\delta _{}}\]
Phasor diagram can be drawn now.












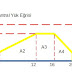


0 Yorumlar