Reaktif Gücün Faydaları

Genelde kurtulunması gereken bir kavram olarak ifade edilen reaktif güç ve buna bağlı reaktif enerjide en iyi analoji bira köpüğünden ziyade bence el arabası örneğidir. El arabasını kollarından tutup kaldırmak reaktif gücü ve ittirerek hareket ettirmek aktif gücü temsil eder. Reaktif güç olmadan yani el arabasını kaldırmadan ittirmek çok kolay değildir. Şebekede reaktif güç bulunmalıdır.

Reaktif güç indüktif reaktif  kapasitif reaktif güç olarak ayrılır. Manyetik veya elektrik alan olarak enerji depolama yani reaktif güç tüketme indüktif reaktif  ve depolanan enerjiyi salarak reaktif güç verme ya da reaktif güç üretme kapasitif reaktif olarak adlandırılır. Trafolar ve motorlar, endüktif yüklerdir ve manyetik alan oluşturmak için enerjiye ihtiyaç duyulduğundan indüktif reaktif güç çekerler.

Reaktif güç :

\[Q = {V_{rms}}{I_{rms}}\sin \varphi \]

Akım

\[i(t) = {I_{\max }}cos(\omega t)  \]

olsun.

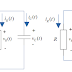
Bir indüktör ya da bobinde gerilim:

\[{v_L}(t) = L\frac{{di(t)}}{{dt}} =  - L\omega {I_{\max }}\sin (\omega t)\]

Bobinde depolanan manyetik enerji:

\[ {W_L}(t) = \frac{1}{2}Li{(t)^2} = \frac{1}{2}LI_{\max }^2{\cos ^2}(\omega t) \]

Kosinüs ifadesi ile birlikte bu enerji sinusoidal ve periyodik olarak değişir. Depolanan manyetik enerjinin maksimum değeri :

\[{W_{L,{\rm{max}}}} = \frac{1}{2}LI_{\max }^2\]

İndüktif Reaktans

\[{X_L} = \omega L = 2\pi fL\]

Anlık güç:

\[{p_L}(t) = {v_L}(t) \cdot i(t) =  - L\omega {I_{\max }}\sin (\omega t) \cdot {I_{\max }}\cos (\omega t) =  - \frac{1}{2}L\omega I_{\max }^2\sin (2\omega t)\]

Ortalama reaktif güç:

\[{Q_L} = {\left( {\frac{{{I_{\max }}}}{{\sqrt 2 }}} \right)^2} \cdot \omega L = \frac{{I_{\max }^2\omega L}}{2} = I_{{\rm{rms}}}^2 \cdot {X_L}\]

\[\sin \varphi  = 1\]

\[{Q_L} = {V_{{\rm{rms}}}}{I_{{\rm{rms}}}}\]

Bobin gerilimi

\[{V_{{\rm{rms}}}} = {I_{{\rm{rms}}}} \cdot {X_L}\]

\[{Q_L} = I_{{\rm{rms}}}^2 \cdot {X_L}\]

Bobin ya da indüktörün reaktif gücü frekans bileşeni nedeniyle enerji depolama hızıyla orantılı olur ve pozitif işaretli olduğundan reaktif enerji çeker

Kapasitör ya da kondansatör, elektrik alanda enerji depolar ve bu enerji, gerilimin zamana bağlı değişimiyle ilişkilidir.

\[v(t) = {V_{\max }}\cos (\omega t)\]

Kapasitör akımı:

\[{i_C}(t) = C\frac{{dv(t)}}{{dt}} =  - C\omega {V_{\max }}\sin (\omega t)\]

Kapasitörde zamana bağlı  enerji

\[{W_C}(t) = \frac{1}{2}Cv{(t)^2} = \frac{1}{2}CV_{\max }^2{\cos ^2}(\omega t)\]

Maksimum enerj

\[{W_{C,{\rm{max}}}} = \frac{1}{2}CV_{\max }^2\]

Kapasitif reaktans:

\[{X_C} = \frac{1}{{\omega C}} = \frac{1}{{2\pi fC}}\]

Zamana bağlı anlık güç

\[{p_C}(t) = v(t) \cdot {i_C}(t) = {V_{max}}\cos (\omega t) \cdot ( - C\omega {V_{\max }}\sin (\omega t)) =  - \frac{1}{2}C\omega V_{\max }^2\sin (2\omega t)\]

 \[- \frac{1}{2}C\omega V_m^2\sin (2\omega t) =  - \frac{1}{{2{X_C}}}V_{\max }^2\sin (2\omega t)\]

\[{Q_C} =  - \frac{{V_{{\rm{rms}}}^2}}{{{X_C}}}\]

Negatif işaret nedeniyle kapasitif reaktif verir.

Asenkron motor stator ve rotor arasında dönen manyetik alan oluşturmak için reaktif güç çeker. Stator sargıları, manyetik akı üretmek için endüktif bir empedansa sahiptir, bu da akımın gerilimden geri kalmasına (faz farkı) neden olur. Stator sargılarından geçen akım döner bir manyetik alan oluşturur ve rotoru döndürerek mekanik enerji üretir.

Manyetik alanın oluşması için stator endüktansı reaktif güç tüketir.

\[{Q_L} = I_{{\rm{rms}}}^2 \cdot {X_L}\]

Trafolar, çekirdekte manyetik akı oluşturmak için magnetizasyon akımı çeker, bu da reaktif güç tüketimi oluşturur. Sargı endüktansından dolayı indüktiftir. Magnetizasyon akımı reaktif güç oluşturur.

\[{Q_m} = \frac{{{V_{primer}}^2}}{{{X_m}}} = \frac{{{V_{primer}}^2}}{{\omega {L_m}}}\]

Reaktif enerji olmadan transformatör manyetik akı oluşturamaz ve sekonder gerilim oluşmadığıdan gerilimi istenen seviyeye getiremez.

Şebekede de gerilim regülasyonu veya akım sınırlaması için indüktör ya da reaktör kullanılarak doğrudan reaktif güç çekilir ve gerilim düşürülür, Şebekelerde, özellikle uzun iletim hatlarında veya hafif yük koşullarında, hatların kapasitif etkisi (kapasitans) nedeniyle gerilim yükselmeleri meydana gelebilir (Ferranti etkisi). Şönt reaktörler, bu fazla kapasitif reaktif gücü absorbe ederek gerilimi düşürür. Seri reaktörler, kısa devre akımlarını sınırlandırır bununla birlikte reaktif güç çeken seri reaktöre hat empedansını artırır güç akışını kontrol eder.

\[{Z_{{\rm{toplam}}}} = R + j{X_L}\]

\[P = \frac{{{V_1}{V_2}\sin (\delta )}}{{\mid Z\mid }}\]

Reaktans artışı aktif gücü azaltır yüklenmeyi önler.

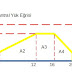
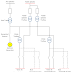
Reaktif güç, şebekedeki gerilim düşüşlerini önleyerek sistemin gerilim kararlılığını artırır. Örneğin, kapasitör bankaları veya senkron kompanzatörler uzun iletim hatlarında oluşan indüktif gerilim seviyesini sabit tutmak için kullanılır. Şebekede gerilim düşümü ( V azalması) enerji kayıplarına basitçe MWh=VI.h ve akımı etkileyerek ekipman arızalarına yol açabilir.Güneş panelleri veya rüzgar türbinlerinde, invertörler reaktif güç sağlayarak şebeke gerilimini destekleyebilir.

Tip 1: Sabit Hızlı, Asenkron Jeneratörlü rüzgar türbini rotor manyetizması için reaktif güç çeker. Tip 2 (WRIG) de harici dirençler reaktif güç ihtiyacını bir miktar azaltır ancak reaktif güç çeker.Tip 3 (DFIG) de güç elektroniği sayesinde reaktif güç üretimi veya tüketimi kontrol edilebilir. Yüksek yük veya düşük gerilim koşullarında reaktif güç çekebilir.Tip 4 (PMSG/WRSG) ise güç elektroniği ile reaktif güç verebilir.

https://electricterms.blogspot.com/2021/06/reaktif-guc-ve-gerilim-iliskisi.html