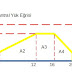
Omik, kapasitif, indüktif devrelerde anlık güç formulü çıkarılışından önce bilinmesi gereken ve kitaplarda formül geçişlerinde sıkıntı olabilecek konu bir sinüs dalgasında ortalama değer hesabıdır. Detaylandırma için Şekil 1'de bir sinüs dalgasında ( bu bir anlık gerilim eğrisi olabilir) çizgilerin altında (alternans) kalan alanların hesabı gösterilmektedir. Formül geçişlerinde yorucu olmaması açısından uzun işlem yapılmıştır.
 |
| Şekil 1. Anlık Gerilim Sinüsoidal Eğri Altında Kalan Alanlar |
Seçilen yerdeki yarım periyodun alanı için:
\[\int {\sin \theta = - \cos \theta }\]
\[Ala{n_{Yar\imath mPeriyot}} = \int\limits_0^\pi {{V_{\max }}.\sin \theta .d\theta }\]
\[= {V_{\max }}.\left[ { - \cos \theta } \right]_0^\pi = - {V_{\max }}.\left[ {\cos \pi - \cos 0} \right]\]
\[= - {V_{\max }}( - 1 - 1) = 2{V_{\max }}\]
y eksenin yani gerilim değeri eksenin negatif tarafında bulunan eğri için de alan benzer şekilde hesaplanabilir.
\[Ala{n_{Yar\imath mPeriyot}} = \int\limits_\pi ^{2\pi } {{V_{\max }}.\sin \theta .d\theta }\]
\[= - {V_{\max }}.\left[ {\cos 2\pi - \cos \pi } \right] = - {V_{\max }}(1 + 1) = - 2{V_{\max }}\]
Alanlar toplamı birbirini götürdüğü için bir tam periyotta toplam alanın sıfır olduğu ortaya çıkmaktadır. İntegral ile işlem yapıldığında da benzer sonuç ortaya çıkar.
\[Ala{n_{TamPeriyot}} = \int\limits_0^{2\pi } {{V_{\max }}.\sin \theta .d\theta }\]
\[= - {V_{\max }}(\cos 2\pi - \cos 0) = - {V_{\max }}(1 - 1) = 0\]
Anlık Gerilimin Ortalama Değeri
Simetrik bir sinüs eğrisinin ortalama değeri için eğri altında kalanlar kullanılabilir.
\[Ortalama = \frac{{Ala{n_{tamperiyot}}}}{{Uzunlu{k_{tamenperiyot}}}}\]
veya
\[Ortalama = \frac{{Ala{n_{Yar\imath mPeriyot}}}}{{Uzunlu{k_{Yar\imath mPeriyot}}}}\]
ile hesaplanabilir. Periyot uzunluğu yarım veya tam olabilmektedir. Yarım periyot alternans dikkate alındığında anlık gerilimi ifade eden sinüs fonksiyonu ortalama değeri gerilimin maksimun değerinin yaklaşık %63'ü olmaktadır. Dikkat edilirse yarım periyot uzunluğu
\[\pi\]
radyan
ya da 3,14 alınmaktadır.
\[{V_{ortalama}} = \frac{{2{V_{\max }}}}{\pi } = \frac{2}{{3,14}}{V_{\max }} = 0,637.{V_{\max }}\]
Tam periyotta da benzer şekilde; tam periyot 2*pi alınsa bile eğri altındaki alan zaten sıfır olduğundan sinüs fonksiyonun ( kosinüs de olabilir) bir periyot boyunca ortalama değeri sıfır olur.
\[{V_{ortalama}} = \frac{0}{{2\pi }} = 0\]
Bu değerin excelde zaman değeri girilerek anlık değer olarak ifade için aşağıdaki video izlenebilir. Açı formundan
\[ \theta\]
tek tek zaman değeri girilip excelde de
\[\omega t = 2\pi ft\]
olarak değer verilip konu detaylandırılabilir.








0 Yorumlar